SGD, Adam and Weight Decay
Optimization lies at the core of deep learning. And despite that how much time to we spend thinking about which optimizer to use when training the latest neural network? This blog post arose from me seeing the AdamW optimizer being used in paper on data-efficient image transormers and then looking for answers to the question: what is AdamW?
SGD, Momentum and Adam
Before we get to AdamW, let us first revisit the basics, if for no other purpose than to fix notation. Given an objective function \(f(\theta)\), depending on some parameters \(\theta\), that we want to minimize, stochastic gradient descent (SGD) performs the parameter update
\[\theta_{t+1} = \theta_t - \alpha g_t\,,\]where \(g_t = \nabla f(\theta_t)\) is the gradient of \(f\) and \(\alpha\) the learning rate.
The name stochasctic comes from the fact the function we would like to minimize is the average loss \(F(\theta) = \mathbb E_{x~D}[\ell(x|\theta)]\), with the expectation taken over some data distribution \(D\). But this expectation is computationally intractable and we approximate it with the empirical loss \(f(\theta) = \frac 1N \sum_{i=1}^N \ell(x_i | \theta)\) over a minibatch \((x_1, \dots, x_N)\). If we assume that the minibatch is sampled randomly, then the empirical gradient becomes a stochastic estimate for the true gradient.
Coming back to SGD, we see from the formula that the algorithm has no memory. The update at step \(t\) depends only on the gradient at that \(\theta_t\). Momentum is a method to stabilise SGD and to prevent oscillating behaviour. It does so using a moving average of the gradient for the parameter update
\[\begin{aligned} m_{t} &= \beta m_{t-1} + (1 - \beta) g_t \\ \theta_{t+1} &= \theta_t - \alpha m_{t}\,. \end{aligned}\]The parameter \(\beta\) is usually set to 0.9.
Both SGD and SGD with momentum are methods with a fixed learning rate. Adam, first proposed by Kingma and Ba is a first-order method that adapts the learning rate based on the second order moment of gradient. We start with the update formula
\[\begin{aligned} m_t &= \beta_1 m_{t-1} + (1 - \beta_1) g_{t} \\ v_t &= \beta_2 v_{t-1} + (1 - \beta_2) g_{t}^2 \\ \hat m_t &= m_t / (1 - \beta_1^t) \\ \hat v_t &= v_t / (1 - \beta_2^t) \\ \theta_{t+1} &= \theta_t - \alpha \frac{\hat m_t}{\sqrt{\hat v_t} + \varepsilon} \end{aligned}\]The variable $m_t$ is a moving average of the gradient as before, while $v_t$ is a moving average of the uncentered second moment, i.e., the point-wise product \(g_t^2 = g_t \odot g_t\). Next \(\hat m_t\) and \(\hat v_t\) are bias corrections: for large \(t\)we have \(\hat m_t \approx m_t\) and \(\hat v_t \approx v_t\), but for small \(t\) they correct for the initialization bias \(m_0 = 0\) and \(v_0 =0\). Finally, we update weights using the rescaled gradient \(m_t / (\sqrt{\hat v_t} + \varepsilon)\).
\(L^2\)-regularization or weight decay?
\(L^2\)-regularization is a classic method to avoid overfitting. We add the \(L^2\)-norm of the weights to the loss function \(f\),
\[\tilde{f}(\theta) = \mathcal f(\theta) + \frac{\eta}{2} \| \theta \|^2\,,\]and we optimize the modified loss \(\tilde{f}\) instead. The term weight decay comes from the observation that the SGD update for the modified loss is
\[\begin{aligned} \theta_{t+1} &= \theta_t - \alpha g_t - \alpha \eta \theta_t \\ &= (1 - \alpha \eta) \theta_t - \alpha g_t \,, \end{aligned}\]with \(g_t = \nabla f(\theta_t)\) being the gradient of the loss function as before. Compared to the SGD update for the original loss, \(\theta_{t+1} = \theta_t - \alpha g_t\) we see that the weights are reduced in each step by a factor of \((1-\alpha\eta)\), hence the term weight decay.
However, as observed by Loshchilov and Hutter 2017, this relationship between \(L^2\)-regularization and weight decay only holds for SGD. As soon as we modify the optimizer, e.g., by adding weight decay, the two concepts diverge. When using momentum, the parameter update using weight decay is still
\[\begin{aligned} m_{t} &= \beta m_{t-1} + (1 - \beta) g_t \\ \theta_{t+1} &= \theta_t - \alpha m_{t} - \alpha \eta \theta_t \,. \end{aligned}\]On the other hand, the update step for \(L^2\)-regularization becomes
\[\begin{aligned} m_{t} &= \beta m_{t-1} + (1 - \beta) (g_t + \eta \theta_t) \\ \theta_{t+1} &= \theta_t - \alpha m_{t} \,. \end{aligned}\]Instead of substracting \(\alpha\eta \theta_t\) from the current weights, we modify the momentum by \((1 - \beta) \eta \theta_t\) and then the modified momentum is used to update the weights.
Practical implications
Now that we know that the two formulations are different, which one shall we choose?
Sylvain Gugger and Jeremy Howard show in the blog post that Adam with weight decay, short AdamW, outperforms Adam with \(L^2\)-regularization on multiple tasks. In fact the authors didn’t find a task, where \(L^2\)-regularization performs significantly better than AdamW.
Why isn’t AdamW more popular? Part of the reason might be practical. The default implementation in TensorFlow uses \(L^2\)-regularization. In the TensorFlow world AdamW can only be found in the TensorFlow addons package.
And then there is the question: what about all the other optimizers? A literature review by Schmidt et al. 2020 has found more than 100 optimizers, proposed in the last few years. Most optimizers have some hyperparameters that need tweaking and all of them need a learning rate and possibly a learning rate schedule. After a systematic evaluation of 15 optimizers—AdamW unfortunately not among them—they have arrived at the following lessons:
- Optimizer performance varies greatly across tasks.
- Evaluating multiple optimizers with default parameters works approximately as well as tuning the hyperparameters of a single, fixed optimizer.
- While there was no clear winner, Adam remains a strong contender.
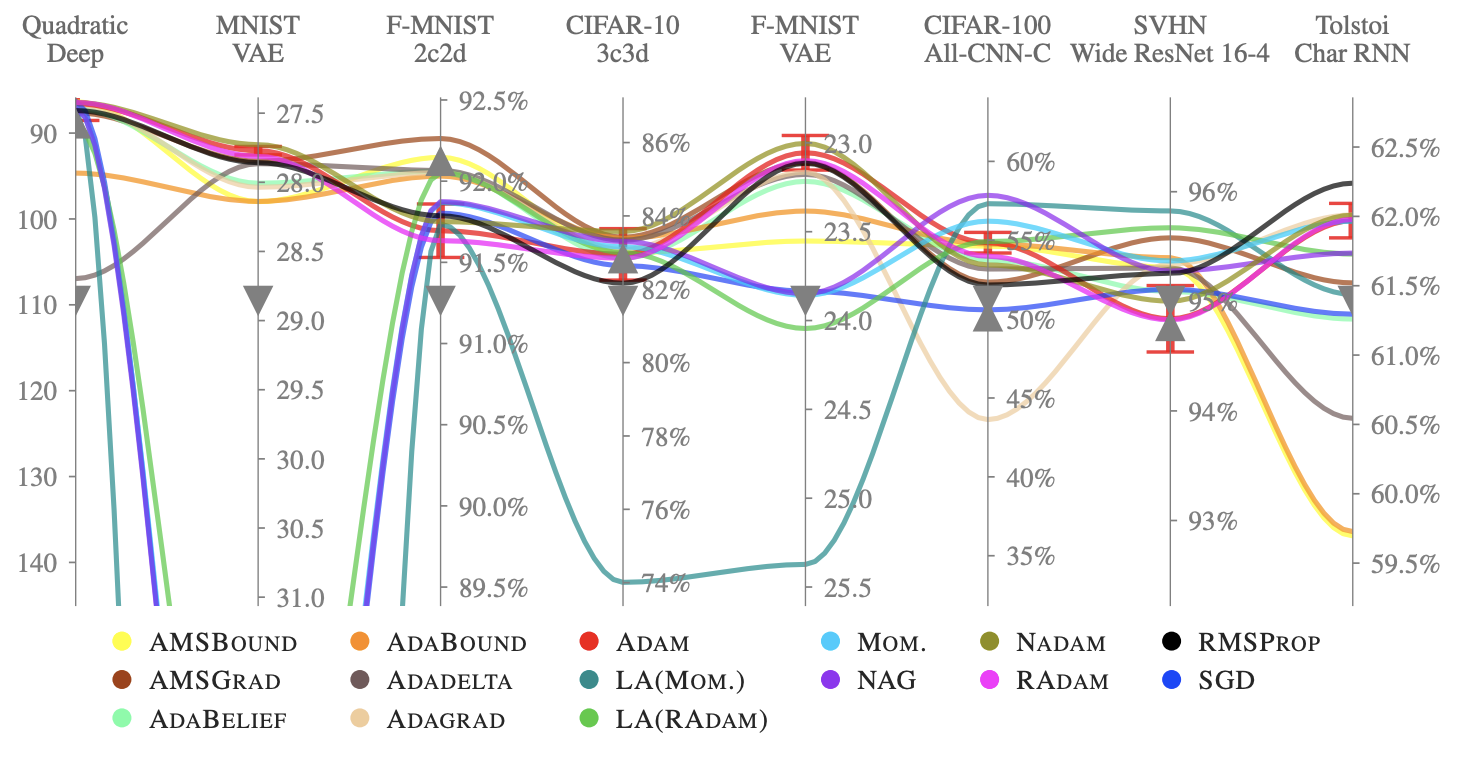
Mean test set performance over 10 random seeds of various optimizers on eight optimization problems after parameter tuning. (Source: Schmidt et al. 2020)
The authors conclude with the following observations
Perhaps the most important takeaway from our study is hidden in plain sight: the field is in danger of being drowned by noise. Different optimizers exhibit a surprisingly similar performance distribution compared to a single method that is re-tuned or simply re-run with different random seeds.
In summary, this was a good opportunity to refresh my knowledge about optimzers. Adam remains a solid choice for the near future and I will try to use AdamW, because it will allow me to skip adding weight regularization to already-built models which in TensorFlow is quite hacky.