Data-Efficient Image Transformers
This is the next post in the series on the ImageNet leaderboard and it takes us to place #71 – Training data-efficient image transformers & distillation through attention. The visual transformers paper showed that it is possible for transformers to surpass CNNs on visual tasks, but doing so takes hundreds of millions of images and hundreds if not thousands of compute-days on TPUs. This paper shows how to train transformers using only ImageNet data on GPUs in a few days.
Knowledge distillation
There are two ingredients: knowledge distillation and careful choice of hyper-parameters and data augmentation. First, the authors observe that knowledge distillation, either from a CNN or another transformer, results in better accuracy than training just on the data. In fact, CNN-supervision performs slightly better than transformer-supervision (see table).
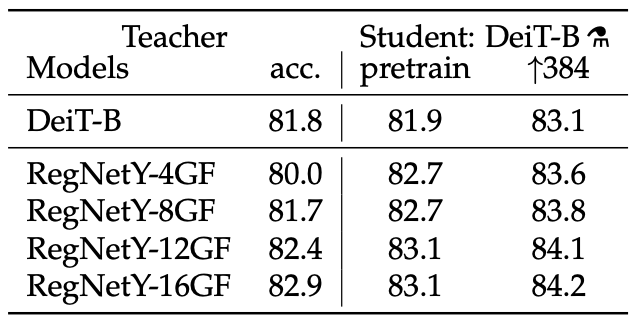
Table 2 from the paper. DeiT-B is the same architecture as ViT-B.
They also introduce a new method to perform knowledge distillation. The distillation token is a transformer-specific change to the model architecture. The input to the transformer consists of the class token and the sequence of flattened patches. The authors add an extra token, the distillation token, to the input sequence. While the output of the class token is used to predict class probabilities, the corresponding output of the distillation token is used specifically to predict the output of the teacher network. This is illustrated in the image below.

Fig. 2 from the paper.
The question arises: why do we need to add a new token? Aren’t all elements in the sequence equal, since attention is global? And doesn’t this mean that we can just use one of the other output tokens for the knowledge distillation loss? In fact, no. Because the attention layers and fully connected layers are part of residual blocks, the tokens keep their identity throughout the layers. Thus the authors are adding a new token with a specific task. They show that adding a new token improves performance compared to using the class token for both tasks (classification and knowledge distillation).
While not a novel part of the paper, the authors also address the question, which loss to choose for the distillation. The two options are hard and soft label distillation with hard distillation being the winner. For completeness sake, here are brief descriptions of the methods. Let \(Z_s, Z_t\) be the logits of the student and teacher networks respectively, \(\psi\) the softmax-function and \(\mathcal L_{\mathrm{CE}}\) the cross-entropy loss.
Hard-label distillation uses the hard label of the teacher model as the true label for the student. Let \(y_t\) be the decision of the teacher model, the objective function is
\[\mathcal L = \frac 12 \mathcal L_{\mathrm{CE}}(\psi(Z_s), y) + \frac 12 \mathcal L_{\mathrm{CE}}(\psi(Z_s), y_t)\,.\]Note that the teacher label can change depending on the specific data augmentation chosen. We can apply label smoothing to hard labels, i.e., the true label is assigned probability \(1 - \varepsilon\) and the remaining \(\varepsilon\) is split among the other classes.
Soft distillation matches the logit distributions of student and teacher using Kullback-Leibler divergence \(\operatorname{KL}\),
\[\mathcal{L} = (1 - \lambda) L_{\mathrm{CE}}(\psi(Z_s), y) + \lambda \tau^2 \operatorname{KL}(\psi(Z_s/\tau), \psi(Z_t/\tau))\,,\]where \(\lambda\) is a coefficient balancing the KL divergence and the cross-entropy loss and \(\tau\) is a temperature parameter.
Data Augmentation
The first visual transformers were trained on the JFT-300 dataset, consisting of 300M images. In this paper the transformers are trained on ImageNet, which is two orders of magnitude smaller. To compensate for this the authors use extensive data augmentation: Rand-Augment, Mixup, CutMix and random erasing.
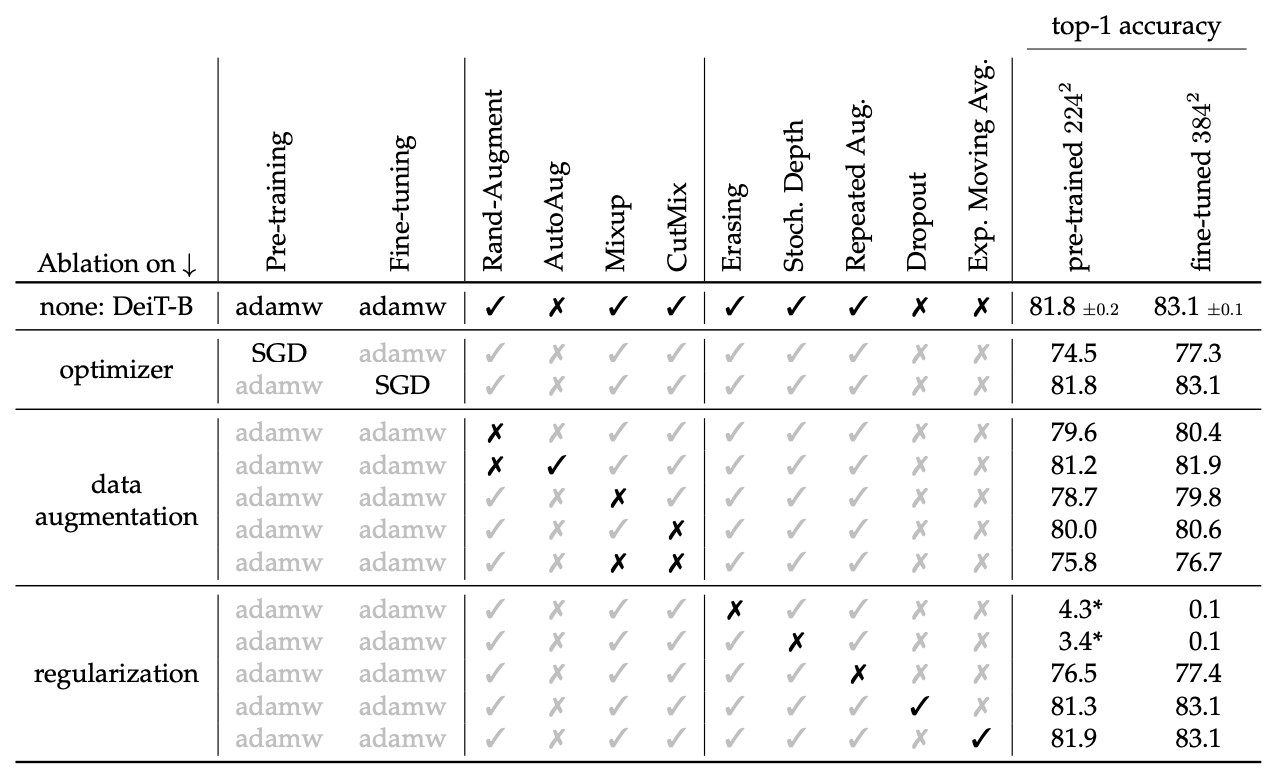
Table 8 from the paper.
Interestingly, they use neither dropout nor exponential weight averaging, both of which were used in the first visual transformers paper. They use AdamW—Adam with weight decay as opposed to L2-regularisation (see this article)—as an optimiser.
Conclusion
What do we take away from this paper? The distillation token is an interesting idea. The transformer architecture makes it easy to add components to the model, in a way that allows information to flow through the whole model. If we want to add another loss to a CNN, we would branch off at one of the later layers. In a transformer, we add a whole column that feeds into the new loss. And data augmentation, when combined with knowledge distillation is able to compensate for a smaller training dataset. And this will—in fact, probably already has—open up the use of transformers beyond the halls of Google.