Going Deeper with Image Transformers
Our journey along the ImageNet leaderboard next takes us to 33rd place and the paper Going Deeper with Image Transformers by Touvron et al., 2021. In this paper they look at tweaks to the transformer architecture that allow them (a) to increase accuracy without needing external data beyond the ImageNet training set and (b) to train deeper transformer models.
Better initialization with LayerScale
The standard transformer block takes the form
\[\begin{aligned} x'_j &= x_j + \mathrm{SA}(x_j) \\ x_{j+1} &= x'_j + \mathrm{FFN}(x'_j)\,, \end{aligned}\]where \(\mathrm{SA}\) is a self-attention module and \(\mathrm{FFN}\) a feed-forward neural network. Other works propose the following modification
\[\begin{aligned} x'_j &= x_j + \alpha_j \mathrm{SA}(x_j) \\ x_{j+1} &= x'_j + \alpha'_j \mathrm{FFN}(x'_j)\,, \end{aligned}\]with learnable parameters \(\alpha\), \(\alpha'\). See papers on Fixup, T-Fixup, ReZero and SkipInit.
In this paper, the authors propose replacing a scalar parameter \(\alpha_j\) with a learnable diagonal matrix \(\Lambda_j = \operatorname{diag}(\lambda_{j, 1}, \dots, \lambda_{j, d})\) and similarly for \(\Lambda'_j\). The transformer block then takes the form
\[\begin{aligned} x'_j &= x_j + \Lambda_j\, \mathrm{SA}(x_j) \\ x_{j+1} &= x'_j + \Lambda'_j\, \mathrm{FFN}(x'_j)\,. \end{aligned}\]The matrices \(\Lambda_j\), \(\Lambda'_j\) are initialized with small values: \(0.1\), \(10^{-5}\) and \(10^{-6}\) for transformers of depth up to 18, 24 and more respectively.
What is the benefit of this initialization? The obvious answer is that it leads to more accurate models. But if we look at the formula for the self-attention block, we see that the matrix \(\Lambda\) is multiplied with the value matrix and in a sense acts as both a near-zero initialization of and a modified learning rate for the value matrix.
Class attention layers
The name CaiT, short for Class Attention in Image Transformers comes from the second modification to the standard transformers architecture. Instead of adding a class token to the input sequence (see figure on the left), the authors add the class token only for the last two layers. Furthermore, after the class token has been added, the patch embeddings are frozen in the final layers (see figure on the right). This effectively divides the network into two phases: first, self-attention on the image patch embeddings, followed by class-attention on the class token with frozen patch embeddings.
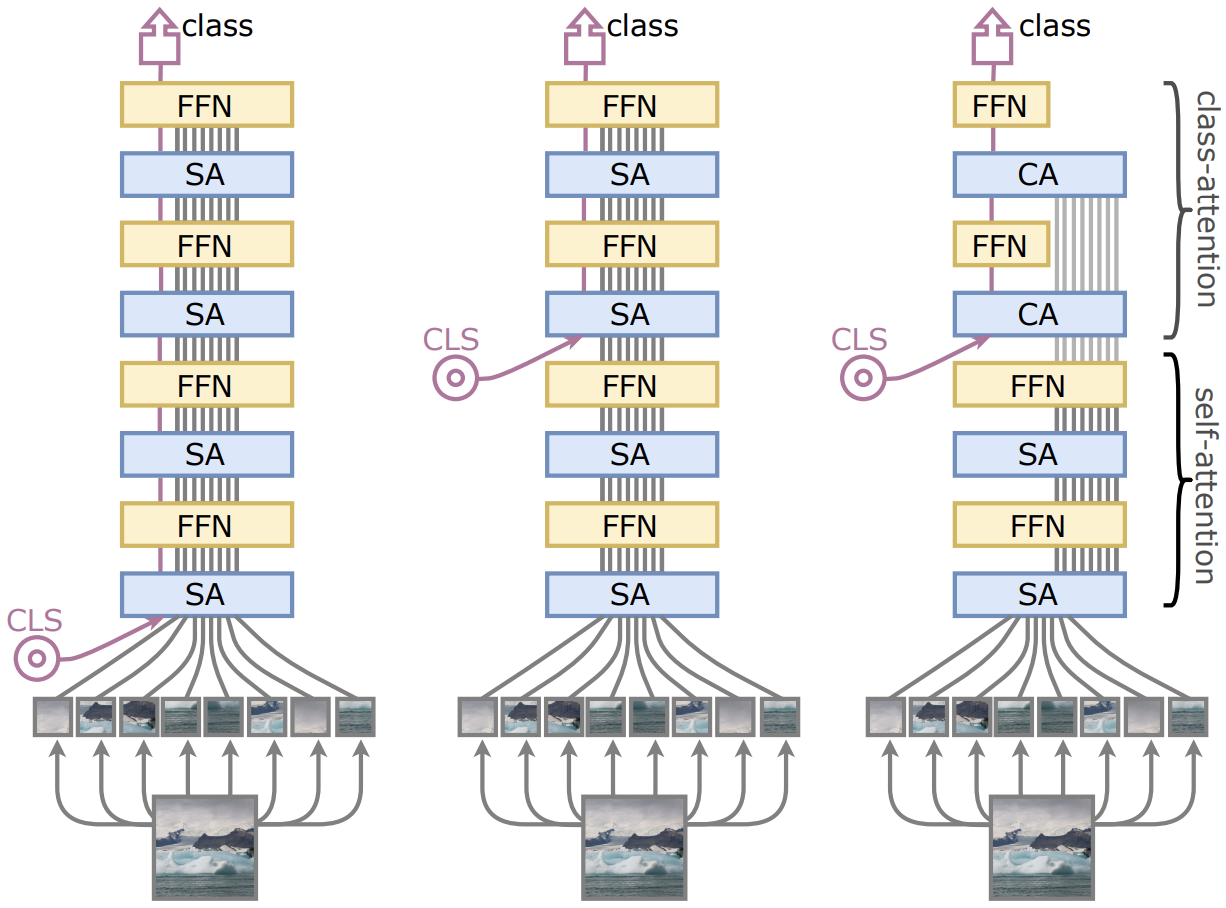
(Source: Fig. 2 in the Touvron et al. 2021)
The authors show that adding the class token late in the network improves performance compared to inserting it at the beginning. They claim that this is because in the traditional architecture
the learned weights are asked to optimize two contradictory objectives: (1) guiding the self-attention between patches while (2) summarizing the information useful to the linear classifier.
I am not convinced by this reason. After all, the only optimization objective for the network is to summarize the information for the linear classifier and the self-attention is only a means for achieving this end. In any case, we can’t argue with the empirical observation.
And this is interesting, because originally I thought that one of the attractions of the transformer architecture is that all information is put on the same footing. As far as the transformer is concerned the image patch is the same as the class embedding or the distillation token or any other type of object. We can think of adding an image description to the input. And all this information gets to interact throughout the network. In a CNN on the other hand, we first have the image information, which is then converted to an embedding after the pooling layer. But it looks like having all the information flow through the network in parallel is not necessarily beneficial for classification. Interesting…
It still leaves the question of the distillation token. The authors mention that they use the same training procedure as in Touvron et al. 2021, including knowledge distillation, which presumably means that the distillation token is added in at the beginning. Or perhaps not. It is hard to say, because the code that the authors published does not include the distillation token for CaiT models.
Talking heads
Instead of multi-head attention the authors use a different attention mechanism, called talking heads. The different flavours of attention layers will probably need a blog post of their own at some point.